This month’s CORE Excellence in Education Blog focuses on the importance of mathematical fluency and number sense as a critical foundation for entering mathematics in middle and high school.

Interested in more great professional insights on mathematical fluency and number sense? Check out this Webinar: Mathematical Fluency and Number Sense: Techniques, Access and Sustainability for All Students

As a mathematics teacher, coach, and consultant I have had the opportunity to work with K-12 students and teachers across the United States, Guam and Japan. The one similarity across all countries is that learning new concepts in math is built on a solid foundation of understanding previous concepts and skills. In my work, the most heart-breaking thing that I observe is students at any grade struggling with new concepts mostly because they cannot do the simple calculations embedded in the work. In many Algebra 1 classes I have painfully watched students count out multiplication facts on their fingers or write out multiples using addition.

Let’s face it, teaching mathematics is challenging at all levels. Each year is filled with new content that is built on prior learning; thus, the time spent teaching basic fluencies is time lost focusing on new concepts. I recently observed my grandniece (whom my sister will tell you is brilliant) count on her fingers 4 + 1. Since she had just completed 1^st grade, I was mortified! I recognize the importance of different counting strategies for building understanding and working toward fluency. However, by the end of first grade my niece should have had 4 + 1 on the tip of her tongue not on the tip of her fingers.

This example illustrates why I am on a mission to improve number sense and fluency in all schools. To this end, the IES Practice Guide, Assisting Students Struggling with Mathematics (2009), recommends providing 10 minutes of daily practice to strengthen needed fluency with facts and procedures (pp. 79-83). Hattie, Fisher and Frey (2017) support this recommendation by documenting that spaced practice, repeated practice of previously learned knowledge over “a long period of time,” has a high effect size of 0.71 (p. 129). In addition, the National Mathematics Advisory Panel (2008) found that fluency with whole numbers and fractions are part of a critical foundation for learning Algebra (pp. 17-18). When I was in high school, it was noted that Algebra 1 was the gate keeper to upper division mathematics. If students weren’t successful in Algebra 1, they would not take higher level math classes. I contend that lack of fluency and number sense are the gate keepers to middle school and high school mathematics.

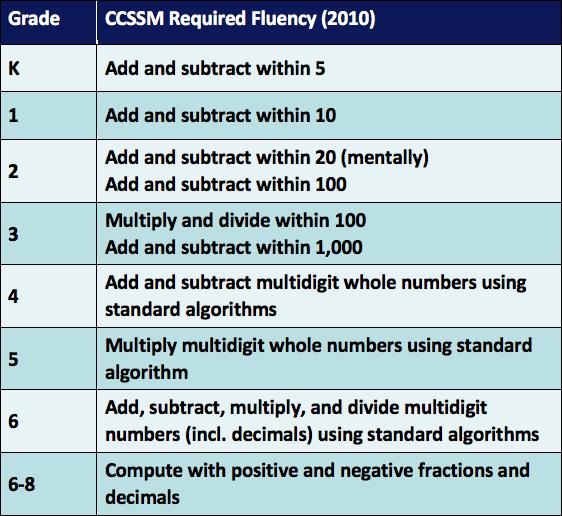
So, what is number sense and what is fluency? The Common Core Standards (CCSSM) describe procedural fluency as “skill in carrying out procedures flexibly, accurately, efficiently and appropriately” (2010). Number sense is making sense of numbers – understanding numbers and how they work together. For example, in the primary grades students understand how numbers can be broken apart and put together when they explore and build fluency with concepts such as how to make 10 and how to break up 12 into 10 and 2. Multiplication builds on this foundation and with multiplication students are introduced to the distributive property: 8 x 12 is the same as 8(10 + 2) = (8 x 10) + (8 x 2). Students apply understanding of these concepts to do mental math, make sense of the standard algorithm for multidigit multiplication, and apply the distributive property in work with algebraic expressions. We want students to build fluency and number sense so that they can continue to understand and solve more complex problems at each new grade level. If students cannot do the “arithmetic” or calculations easily it is difficult for them to solve problems requiring simple calculations. This difficulty is caused by the amount of working memory we have available to us when solving problems. If our working memory is busy trying to figure out the computation, it is more difficult for us to make sense of the higher level mathematical concepts being grappled with at that moment. Similarly, when reading, if students struggle to decode the words, then they will have difficulty understanding the larger meaning of the text. Hence, it is important that students have automaticity with number facts:

Our ability to think would be limited indeed if there were not ways to overcome the space constraint of working memory. One of the more important mechanisms is the development of automaticity. When cognitive processes . . . become automatic, they demand very little space in working memory, they occur rapidly, and they often occur without conscious effort.

Daniel Willingham, 2004

Understanding number relationships and different techniques for putting numbers together and taking them apart are essential parts of building number sense. Automaticity with number facts is equally essential for continued growth in mathematics. As teachers, I believe it is our responsibility to make sure that we are doing everything within our power to ensure students leave our mathematics classroom at the end of the year proficient in the fluency requirements as outlined in the CCSSM and included in all state standards. Anytime a child leaves a grade level without having the required fluency, the mathematical gap begins and continues to grow throughout the years as students fall further behind in their automaticity of facts and understanding of numbers. As we continue to teach mathematics, let’s make sure we are doing our part to teach the fluencies needed at each grade level.

References

Gersten, R., Beckmann, S., Clarke, B., Foegen, A., Marsh, L., Star, J. R., & Witzel, B. (2009). Assisting Students Struggling with Mathematics: Response to Intervention (RtI) for Elementary and Middle Schools (NCEE 2009-4060 ed.). Washington, DC: National Center for Education Evaluation and Regional Assistance, Institute of Education Sciences, U.S. Department of Education. Retrieved from https://ies.ed.gov/ncee/wwc/PracticeGuide/2

Hattie, J., Fisher, D., & Frey, N. (2017). Visible Learning for Mathematics. Thousand Oaks, CA: Corwin.

National Governors Association Center for Best Practices & Council of Chief State School Officers. (2010). Common Core State Standards for Mathematics. Washington, DC: Authors.

National Mathematics Advisory Panel. (2008). Foundations for Success: The Final Report of the National Mathematics Advisory Panel. Washington, DC: U.S. Department of Education. Retrieved from https://www2.ed.gov/about/bdscomm/list/mathpanel/report/final-report.pdf

Willingham, D. T. (2004, Spring). Practice Makes Perfect—but Only If You Practice Beyond the Point of Perfection [Electronic version]. American Educator. doi: https://www.aft.org/periodical/american-educator/spring-2004/ask-cognitive-scientist

To receive future editions of this blog via e-mail, add your name to the mailing list.